
Trong thực tế, ta cần áp dụng nhiều thuật toán Machine learning để chọn ra được mô hình phù hợp nhất cho bài toán của mình. Vấn đề đặt ra, làm thế nào để đánh giá và chọn ra các mô hình. Ngoài thuật toán học máy, sự thực thi của mô hình có thể phụ thuộc vào các yếu tố khác như sự phân bố của các lớp, chi phí phân loại sai, kích thước của tập huấn luyện và tập thử nghiệm, độ đo thực thi. Trong bài viết này, ta sẽ đánh giá thực thi: tập trung vào khả năng dự đoán của mô hình hơn là tốc độ phân loại hay xây dựng mô hình, khả năng co giãn.
Confusion matrix
| Predicted Class | |||
| Actual Class | Yes | No | |
| Yes | a | b | |
| No | c | d | |
Đầu tiên, ta hãy làm quen với confusion matrix (ma trận nhầm lẫn).
Quan sát confusion matrix, ta có các thông tin sau:
- a:TP (true positive) – mẫu mang nhãn dương được phân lớp đúng vào lớp dương.
- b:FN (false negative) – mẫu mang nhãn dương bị phân lớp sai vào lớp âm.
- c:FP (false positive) – mẫu mang nhãn âm bị phân lớp sai vào lớp dương.
- d:TN (true negative) – mẫu mang nhãn âm được phân lớp đúng vào lớp âm.
Từ đây, đô chính xác của mô hình M được tính như sau:
Độ lỗi của mô hình M được tính như sau:
Ngoài ra, ta còn một số độ đo khác:

Phương pháp Hold-out

Phương pháp Hold-out phân chia tập dữ liệu thành 2 tập độc lập. Ví dụ, tập huấn luyện (training set) 2/3, tập thử nghiệm (testing set) 1/3.
Phương pháp này thích hợp cho các tập dữ liệu nhỏ. Tuy nhiên, các mẫu có thể không đại diện cho toàn bộ dữ liệu (thiếu lớp trong tập thử nghiệm).
Ta có thể cải tiến bằng cách dùng phương pháp lấy mẫu sao cho mỗi lớp được
phân bố đều trong cả 2 tập dữ liệu huấn luyện và thử nghiệm. Hay lấy mẫu ngẫu nhiên : thực hiện holdout k lần và độ chính xác acc(M) = trung bình cộng k giá trị chính xác.
Phương pháp Cross validation
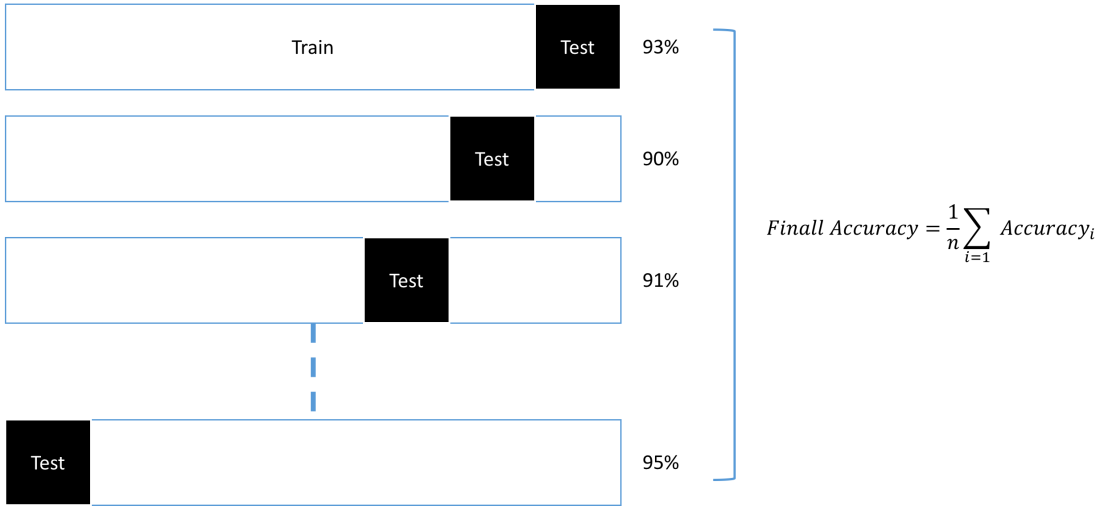
Hay còn gọi là k-fold Cross validation. Phương pháp này phân chia dữ liệu thành k tập con có cùng kích thước. Tại mỗi vòng lặp sử dụng một tập con là tập
thử nghiệm và các tập con còn lại là tập huấn luyện. Giá trị k thường là = 10. Ta có thể dùng một trong hai cách:
- Leave-one-out : k=số mẫu trong dữ liệu (dành cho tập dữ liệu nhỏ)
- Stratified cross-validation : dùng phương pháp lấy mẫu để các lớp trong từng tập con phân bố như trên toàn bộ dữ liệu.
Confident Interval
Khoảng tin cậy được sử dụng để đánh giá độ tin cậy của một ước lượng thống kê. Khoảng tin cậy có phương sai lớn, nghĩa là mô hình của bạn không được tốt (cần phải thực nghiệm các mô hình khác), hoặc số lượng dữ liệu bị nhiễu nhiều nếu khoảng tin cậy không cải thiện khi đã thử nghiệm ở nhiều mô hình khác. Xem thêm ở video phía trên để hiểu hơn về độ đo này.
Gain and Lift Chart
Lift là một độ đo về hiệu quả của một mô hình dự đoán được tính bằng tỷ số giữa kết quả thu được trong trường hợp có và không có mô hình dự đoán. Gain và Lift chart là phương tiện trực quan để đánh giá mô hình. Cả hai biểu đồ này đều gồm có đường cong lift và baseline (đường cong để đối chiếu trước và sau khi áp dụng mô hình). Xem thêm ở video phía trên để hiểu hơn về độ đo này.
Kolmogorov-Smirnov Chart
Là kiểm định thống kê non-parametric được dùng để so sánh hai phân phối, để đánh giá mức độ gần gũi giữa chúng. Trong bối cảnh này, một trong hai phân phối là phân phối lý thuyết (thường là một phân bố liên tục với một hoặc hai tham số, chẳng hạn như phân phối Gauss), trong khi phân phối còn lại là phân phối trong thực tế, thực nghiệm, phi tham số, phân phối rời rạc được tính dựa trên quan sát. Xem thêm ở video phía trên để hiểu hơn về độ đo này.
Chi Square
Là một phép kiểm định thống kê tương tự như Kolmogorov-Smirnov, nhưng trong trường hợp này nó là một parametric test. Phép kiểm định này đòi hỏi bạn phải tổng hợp các quan sát theo buckets hay bins, với ít nhất 10 quan sát ở mỗi bin. Xem thêm ở video phía trên để hiểu hơn về độ đo này.
Đường cong Receiver Operating Characteristic (ROC)
Không giống như biểu đồ lift, đường cong ROC gần như độc lập với response rate. ROC là một đồ thị minh họa hiệu suất của một hệ thống phân loại nhị phân khi thay đổi ngưỡng phân lớp. Đường cong được tạo ra bằng cách vẽ tỷ lệ true positive (TPR) so với tỷ lệ false positive (FPR) các thiết lập ngưỡng khác nhau. TPR cũng được biết đến như độ đo sensitivity hay chỉ số sensitivity d, còn gọi là “d-prime” trong tác vụ phát hiện tín hiệu và tin sinh học, hoặc recall trong Machine Learning. FPR cũng được biết đến như fall-out và có thể được tính bằng công thức (1 – specificity). Đường cong ROC thể hiện quan hệ giữa sensitivity và hàm fall-out. Xem thêm ở video phía trên để hiểu hơn về độ đo này.
- Animations with receiver operating characteristic curve (ROC curve)
- Calculating AUC: the area under a ROC Curve
Gini Coefficient
Hệ số Gini đôi khi được dùng trong đánh giá mô hình classification. , trong đó AUC là diện tích phía dưới đường cong (xem thêm đường cong ROC ở trên). Tỷ lệ Gini trên 60% tương ứng với một mô hình tốt. Không nên nhầm lẫn chỉ số Gini hay độ hỗn độn Gini impurity, được sử dụng khi xây dựng cây quyết định. Xem thêm ở video phía trên để hiểu hơn về độ đo này.
Root Mean Square Error (RMSE)

Gía trị bình phương trung bình lỗi lấy căn thường xuyên được sử dụng trong đánh giá độ khớp của mô hình so với dữ liệu huấn luyện. Được tính bằng căn bậc hai của giá trị tuyệt đối của hệ số tương quan giữa giá trị thực và giá trị dự đoán.
Kết luận
Phân lớp là hình thức phân tích dữ liệu để rút ra các mô hình mô tả các lớp dữ liệu quan trọng. Không thuật toán nào vượt trội nhất cho mọi tập dữ liệu. Dựa vào các tiêu chí đánh giá như độ chính xác, thời gian huấn luyện, tính linh hoạt, khả năng co giãn,… để có thể đưa ra quyết định sử dụng mô hình nào trong bài toán thực tế.
Tham khảo thêm: